Equilibrio de Nash
El equilibrio de Nash es una situación en la que cada jugador elige la mejor estrategia posible (estrategia dominante) según sus expectativas sobre las acciones del otro jugador. Representa el conjunto de movimientos (m1, m2) en los que la elección de cada jugador es la mejor respuesta a la acción del otro. Los jugadores suponen cuáles serán las decisiones de los demás y, con base en eso, deciden su propia estrategia (“haciendo lo mejor para sí mismos y para los demás”). Un equilibrio de Nash es estable, ya que ningún jugador tiene incentivos para cambiar su decisión (estrategia). Cada jugador busca maximizar su propio beneficio, considerando la mejor opción del otro. Cualquier desviación solo empeoraría su posición (recompensa / utilidad). El equilibrio de Nash es un estado óptimo en un juego no cooperativo, y por eso también se le llama equilibrio no cooperativo. No surge de ningún acuerdo entre los jugadores; más bien, se origina cuando cada jugador adopta estrategias dominantes que aseguran el mejor resultado individual y el equilibrio colectivo. La siguiente matriz de recompensas ilustra un equilibrio de Nash en un juego no cooperativo entre dos jugadores. Aunque este ejemplo se centra en dos jugadores, el concepto puede extenderse a N jugadores.
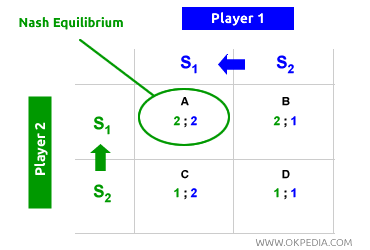
En la matriz, cada jugador puede optar por la estrategia S1 o S2. El jugador S1 espera que el jugador 2 elija S1 (su estrategia dominante) y, por lo tanto, también opta por S1, ya que le proporciona un beneficio individual de 2. De manera similar, el jugador 2 anticipa que el jugador 1 elegirá S1 y también selecciona S1. El equilibrio del juego converge así en la celda A de la matriz (arriba a la izquierda), donde ambos jugadores maximizan sus beneficios individuales (óptimo individual) eligiendo sus estrategias dominantes (equilibrio de Nash). Ambos jugadores suponen cuál será la mejor jugada (estrategia dominante) del oponente y, con base en eso, eligen sus propias estrategias dominantes. El siguiente ejemplo ayuda a entender mejor el proceso de toma de decisiones que lleva al equilibrio de Nash.
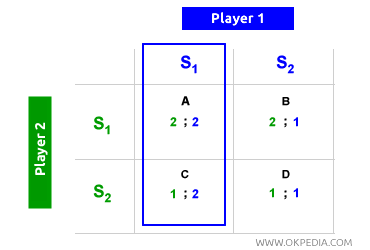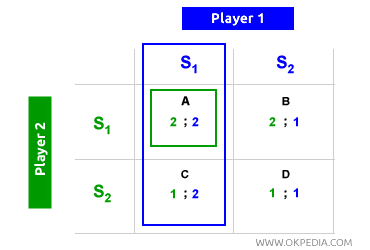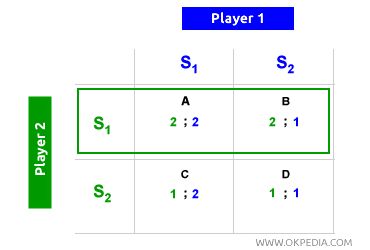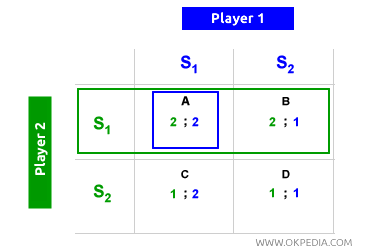
El jugador 1 (verde) puede optar por S1 o S2, y en ambas situaciones busca alcanzar el mayor beneficio (2) que se encuentra en las celdas A y D. Sin embargo, el jugador 1 sabe que si elige S2, el jugador 2 (azul) respondería con S1, estableciendo el equilibrio en la celda C, donde el beneficio para el jugador 1 sería el más bajo (1). Al elegir S1, el jugador 1 sabe que el jugador 2 también encontrará óptimo escoger S1, logrando así un equilibrio en la celda A, donde el beneficio es máximo (2). Aplicando la misma lógica, cuando es el turno del jugador 2 de elegir primero, reconoce que seleccionar S1 hará que el jugador 1 también elija S1, estableciendo nuevamente el equilibrio en la celda A. La celda A es el equilibrio de Nash, mientras que las demás celdas no lo son. En resumen, el equilibrio de Nash se describe a menudo como: “Ganar haciendo lo mejor para uno mismo y para los demás.” Es un concepto clave en la teoría de juegos y en la economía política.
Óptimo social. En un equilibrio de Nash, es posible que ambos jugadores y la sociedad en general alcancen un resultado óptimo. Por ejemplo, cuando el jugador 1 (verde) elige S1 primero, el jugador 2 (azul) también selecciona S1, llevando el equilibrio a la celda A. Cuando el jugador 2 (azul) elige S1 primero, el jugador 1 (verde) también escoge S1, resultando nuevamente en la celda A. Así, la celda A es un equilibrio de Nash. Aquí, ambos jugadores reciben un beneficio de 2 (óptimo individual), y la suma de beneficios (2+2) alcanza 4 (óptimo social). Por lo tanto, en la celda A (equilibrio de Nash), se logra tanto un óptimo individual como uno social.
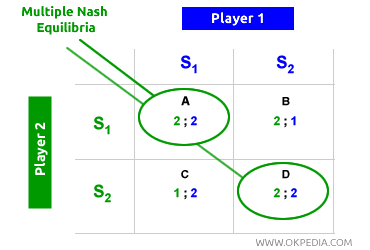
Múltiples equilibrios de Nash. Un juego no cooperativo puede tener varios equilibrios de Nash. Incluso cuando existen múltiples equilibrios, cada uno sigue siendo estable, ya que cualquier desviación empeoraría el resultado para cada jugador. Por ejemplo, la siguiente matriz de beneficios muestra dos equilibrios de Nash simétricos.
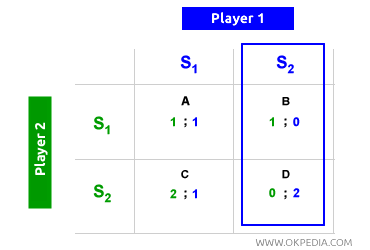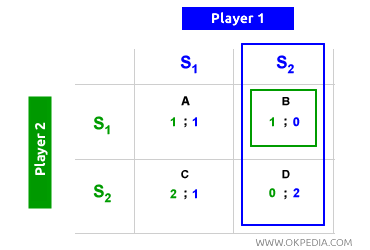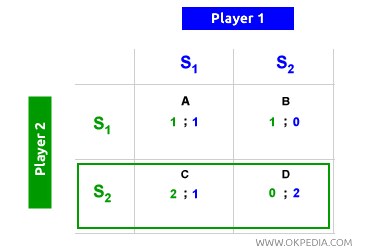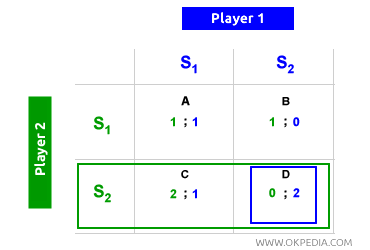
Ausencia de equilibrio de Nash. Otro problema con el equilibrio de Nash es que no siempre existe. Muchos juegos carecen de un equilibrio de Nash. En el ejemplo a continuación, no hay un equilibrio de Nash. Cuando el jugador 1 elige S2, el jugador 2 elige S2, ubicando el equilibrio en la celda D. Sin embargo, cuando el jugador 2 elige S2, el jugador 1 opta por S1, y el equilibrio se traslada a la celda B. Por lo tanto, no existe un equilibrio de Nash en este juego.
Dilema del prisionero. Adoptar estrategias dominantes no siempre garantiza un equilibrio socialmente óptimo. Sin información suficiente, un juego no cooperativo podría terminar en un equilibrio estable pero subóptimo. Esto se ve en el “dilema del prisionero”, donde dos jugadores, incluso haciendo suposiciones racionales sobre las acciones de su oponente y eligiendo estrategias dominantes, acaban en un equilibrio subóptimo (D) tanto a nivel individual como social. El equilibrio D es un equilibrio de Nash pero no un óptimo de Pareto. En conclusión, el equilibrio de Nash y el óptimo de Pareto son conceptos distintos, ya que dependen de condiciones diferentes.
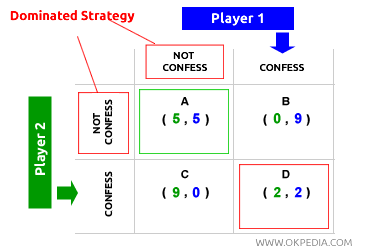
Por ejemplo, el jugador 1 espera que el jugador 2 confiese, ya que confesar es la estrategia dominante del jugador 2. Al confesar, el jugador 2 asegura su libertad (beneficio 9). Basándose en esta expectativa, el jugador 1 elige la opción dominante entre B y D, decidiendo confesar también para garantizar un beneficio de al menos 2. El jugador 2 aplica la misma lógica, pero a la inversa. El equilibrio D es un equilibrio de Nash y se mantiene estable, ya que ningún jugador tiene incentivos para cambiar su decisión. Sin embargo, el equilibrio D no es un óptimo de Pareto, ya que ambos jugadores obtienen un beneficio subóptimo (2) en comparación con el beneficio mayor (5) que recibirían si ambos optaran por no confesar (equilibrio A).
Equilibrio de Cournot. El equilibrio de Nash es un concepto teórico de balance similar al equilibrio de Cournot. En el duopolio de Cournot, cada empresa determina el nivel óptimo de producción con base en la decisión estratégica de su competidor.
