Vectores

Los vectores son magnitudes que se caracterizan por tener tanto dirección como magnitud. En un espacio bidimensional o tridimensional, un vector se representa mediante una flecha de una longitud determinada, que parte de un punto inicial (O) y termina en un punto (x, y).

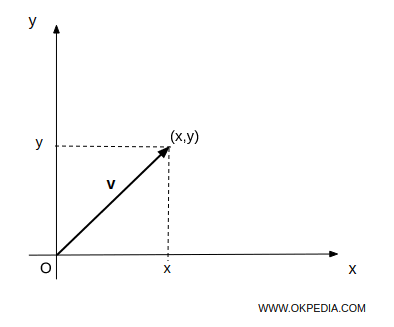
Un vector libre (o simplemente un vector) es un conjunto de segmentos dirigidos equivalentes.

Dos o más segmentos dirigidos son equivalentes cuando comparten la misma magnitud, dirección y sentido.

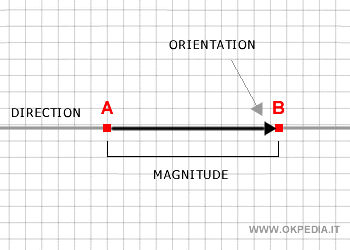
• Magnitud: se refiere a la longitud del vector. Siempre es un valor positivo expresado en una unidad de medida específica.
• Dirección: indica la línea a lo largo de la cual se encuentra el vector.
• Sentido: define la orientación del vector, representada por una flecha.

El estudio de los vectores en dos o más dimensiones forma parte del cálculo vectorial, una rama del álgebra lineal que se enfoca en las magnitudes vectoriales.

¿Qué son las magnitudes vectoriales? Las magnitudes vectoriales se describen mediante una magnitud (longitud o intensidad), una dirección y un sentido. Son distintas de las magnitudes escalares, que se pueden expresar como números reales con una unidad de medida.

Un ejemplo de vector

Los segmentos dirigidos u, v y w pertenecen al mismo vector libre, ya que tienen la misma dirección, sentido y magnitud (longitud).

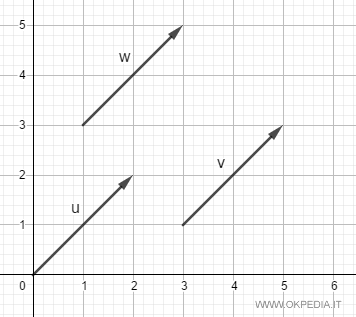
Forman parte de la misma clase de equivalencia.

La única diferencia entre estos tres segmentos dirigidos es su punto de partida.

Vector de posición y vector de desplazamiento

Existen varios conceptos relacionados con los vectores, entre ellos:

• Vector de posición: define la ubicación de un punto en el espacio respecto a un sistema de referencia.
  
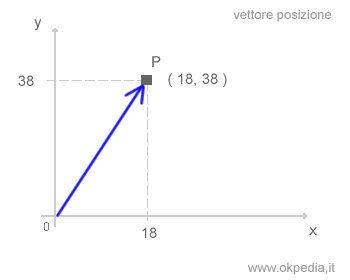
• Vector de desplazamiento: se representa como una flecha que parte de la posición inicial de un punto y apunta hacia su posición final. Indica el cambio en el vector de posición.
  

Operaciones con vectores

Los vectores se pueden someter a distintas operaciones, como la suma, la resta y la multiplicación por un escalar.

Cada operación tiene reglas y propiedades específicas que definen la magnitud y dirección del vector resultante.

Las principales operaciones con vectores incluyen:

• Suma de vectores
  Si (x₁, y₁) y (x₂, y₂) son los extremos de dos vectores, u y v respectivamente, entonces (x₁ + x₂, y₁ + y₂) es el extremo del vector u + v.
  
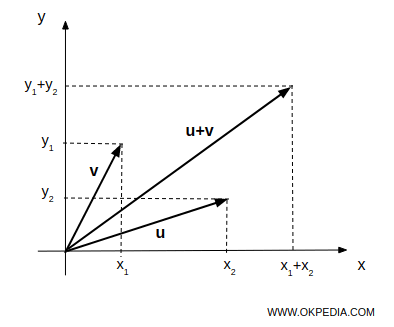
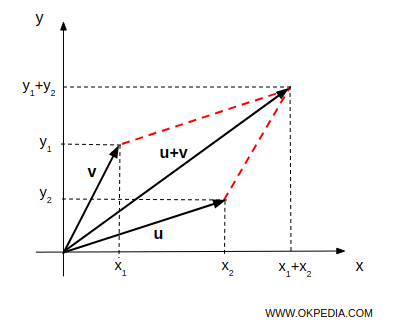
  La suma de dos vectores en el espacio R² = RxR también se puede calcular utilizando el método del paralelogramo.
  
• Multiplicación por un escalar
  Si (x, y) es el extremo del vector v, entonces el producto kv da como resultado un vector con el extremo (kx, ky).
  
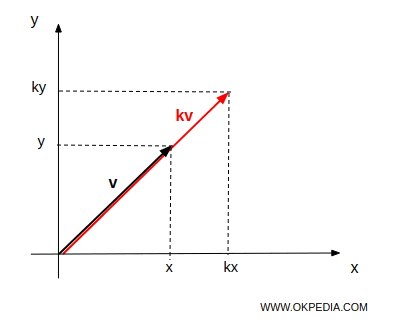
  El producto de un número real k y un vector v se obtiene multiplicando la magnitud de v por k. La dirección permanece igual si k > 0, o se invierte si k < 0.

Vectores en dimensiones superiores

Un vector multidimensional es básicamente una lista ordenada de n valores, que puede conceptualizarse como un n-tupla de números reales. Cada valor se denota por un símbolo con un subíndice que indica su posición en la lista, como x₁, x₂, ..., x_n.

La notación vectorial suele utilizar una letra con una flecha encima, representada como:

$$ \vec{v} = (x_1, x_2, ..., x_n) $$

Los vectores son fundamentales para representar magnitudes que no pueden describirse con un solo valor. En física, la fuerza es un ejemplo claro de una magnitud vectorial.

Nota: En Okpedia, los vectores se distinguen de los escalares al mostrarlos en negrita. Por ejemplo, u, w y v son vectores, mientras que u, v y w representan escalares.