Conjuntos Iguales

Conjuntos Iguales. Se considera que dos conjuntos, A y B, son iguales si contienen exactamente los mismos elementos. Esta relación se denota mediante la ecuación A = B.

Por ejemplo, el conjunto A incluye los elementos {1, 2, 3, 4, 5, 6}, y el conjunto B consta de {1, 2, 3, 4, 5, 6}. Dado que ambos conjuntos poseen los mismos elementos, podemos confirmar que efectivamente son iguales. A continuación se muestra una representación gràfica de conjuntos iguales:

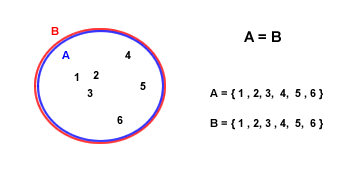
Si dos conjuntos, A y C, no son iguales, esto se indica con A ≠ C. Consideremos, por ejemplo, el conjunto A={1, 2, 3, 4, 5, 6} y el conjunto C={5, 6, 7, 8, 9}. Estos conjuntos no comparten todos los elementos, lo que los hace diferentes y, por tanto, no iguales.

Los conjuntos iguales se caracterizan por una doble inclusión mutua. Los conjuntos A y B son iguales si y solo si el conjunto A està incluido en B y viceversa. Es decir, "dos conjuntos son iguales si cada elemento de uno està también en el otro, y viceversa".

A = B ⇔ A ⊆ B y B ⊆ A

Lo contrario también es cierto. Una condición de doble inclusión mutua se da si y solo si ambos conjuntos son iguales.

Ejemplo 1

Los conjuntos A y B son conjuntos iguales.

$$ A = \{ 1,3,5,7 \} $$

$$ B = \{ 5,1,7,3 \} $$

Cada elemento del conjunto A se encuentra en el conjunto B y cada elemento del conjunto B se encuentra en el conjunto A.

Ejemplo 2

Los conjuntos A y C no son conjuntos iguales.

$$ A = \{ 1,3,5,7 \} $$

$$ C = \{ 5,1,7,4 \} $$

El elemento 3 està en el conjunto A pero no en el conjunto C, y el elemento 4 està en C pero no en A.