Subconjunto
Dado dos conjuntos, A y B, decimos que el conjunto A es un subconjunto del conjunto B si cada elemento de A también pertenece a B.
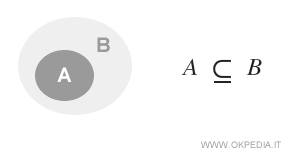
En este caso, el conjunto A está completamente contenido dentro del conjunto B.
En notación matemática, esto se escribe como A ⊆ B y se lee como "el conjunto A es un subconjunto de B" o "el conjunto A está incluido en B".
Ejemplo Práctico
Un subconjunto puede representarse visualmente de la siguiente manera:
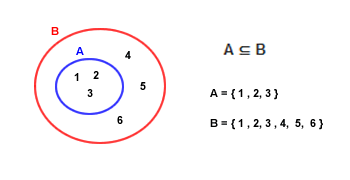
En el diagrama, tenemos dos conjuntos, A y B.
- El conjunto A contiene los elementos { 1, 2, 3 }.
- El conjunto B contiene los elementos { 1, 2, 3, 4, 5, 6 }.
Como puedes ver fácilmente, el conjunto A está contenido dentro del conjunto B. En otras palabras, el conjunto A es un subconjunto de B.
Inclusión Normal vs. Estricta
La relación de subconjunto puede ser normal o estricta.
- Inclusión Normal (A⊆B)
En la inclusión normal, los conjuntos pueden ser iguales (A=B). Incluso podrían ser idénticos.
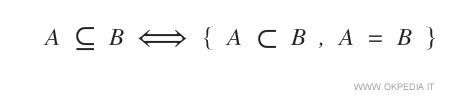
Un subconjunto con una relación de inclusión normal se llama:- subconjunto propio si los dos conjuntos son diferentes (A≠B)
- subconjunto impropio si los dos conjuntos son iguales (A=B) o si el subconjunto está vacío (A=∅).
Ejemplo Práctico
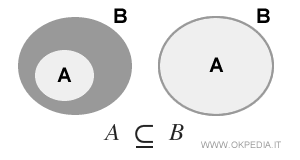
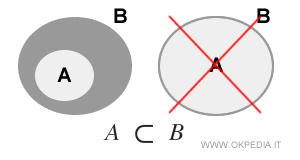
- Inclusión Estricta (A⊂B)
En la inclusión estricta, los conjuntos no pueden ser iguales. Los dos conjuntos son diferentes (A≠B). Por lo tanto, hay elementos en el conjunto B que no están en el conjunto A. En estos casos, decimos que "el conjunto A está estrictamente incluido en B" o "el conjunto A está estrictamente contenido en B", y se denota como A ⊂ B.
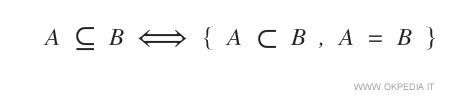
Un subconjunto no vacío con una relación de inclusión estricta siempre es un subconjunto propio porque los dos conjuntos son diferentes.
Ejemplo Práctico
Nota: La inclusión estricta (A⊂B) siempre es también inclusión normal (A⊆B). Sin embargo, la inclusión normal (A⊆B) no es necesariamente inclusión estricta (A⊂B) porque los dos conjuntos podrían ser idénticos.
