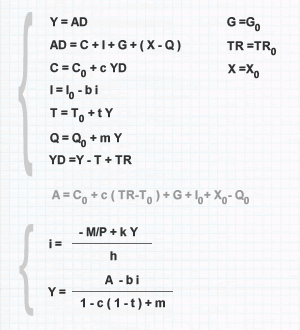Función de Inversión

La función de inversión representa la relación económica entre el volumen de inversiones y la tasa de interés del mercado. Es una parte integral del modelo IS-LM. Existe una relación inversa entre las inversiones y las tasas de interés. Un aumento en la tasa de interés incrementa el costo del dinero. Bajo condiciones similares, para obtener un préstamo, los inversores deben pagar más interés al prestamista. Esto conduce a una disminución en la cantidad de inversiones realizadas por una empresa (gasto de inversión). Por el contrario, una disminución en las tasas de interés tiene el efecto opuesto, reduciendo el costo del dinero y permitiendo a las empresas obtener financiamiento con una menor carga de intereses. Esto anima a los empresarios a aumentar el gasto en inversiones. En el modelo IS-LM, la función de inversión se puede escribir de la siguiente manera:

I = I₀ - b·i

El gasto en inversiones (I) se determina de la siguiente manera. Partiendo del valor de inversión I0, que existiría si la tasa de interés fuera cero (i = 0), restamos la tasa de interés actual (i) multiplicada por la sensibilidad (b) de los operadores económicos a los cambios en la tasa de interés (b > 0). Por ejemplo, con una sensibilidad nula a los cambios en la tasa de interés (b = 0), el gasto en inversiones es independiente de las fluctuaciones de la tasa de interés. Sin embargo, cuando la variable (b) es significativamente alta, el gasto en inversiones se vuelve muy dependiente de los cambios en la tasa de interés. La función de inversión puede representarse gráficamente en un diagrama cartesiano, trazando los valores de inversión en el eje x y la tasa de interés en el eje y.

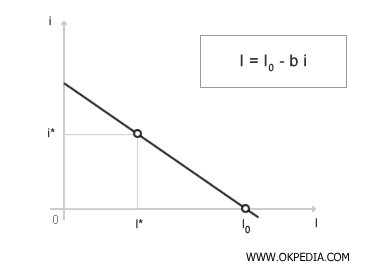
En un plano cartesiano, la función de inversión muestra una tendencia decreciente. Un aumento en la tasa de interés (i) reduce el gasto en inversiones (I) de las empresas, y viceversa. El punto de intersección I0 en el eje x indica el valor de inversión si la tasa de interés fuera cero (i = 0). Por ejemplo, una tasa de interés i* conduce a un gasto en inversiones I*. La representación gráfica también permite un análisis más detallado de la sensibilidad (b) a los cambios en la tasa de interés. El siguiente diagrama ilustra dos casos contrastantes:

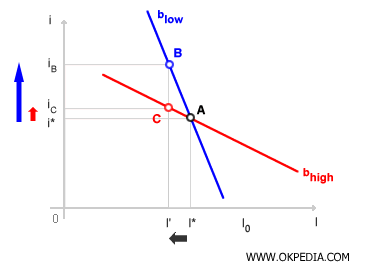
En la función de inversión con alta sensibilidad (b_alta), un pequeño cambio en la tasa de interés provoca una variación significativa en el gasto en inversiones (I). La función de inversión se muestra casi plana. Por el contrario, en la función de inversión con baja sensibilidad (b_baja), un cambio en la tasa de interés conduce a una variación mínima en el gasto en inversiones. La demanda de inversiones es más rígida. Por ejemplo, para reducir las inversiones de I* a I', en la función de inversión altamente sensible (b_alta), solo se requiere un pequeño cambio en la tasa de interés de i* a i_C. El equilibrio se desplaza del punto A al C. En la función de inversión menos sensible (b_baja), sin embargo, se necesita un cambio significativo en la tasa de interés de i* a i_B ya que las decisiones de inversión de las empresas están menos influenciadas por el nivel de la tasa de interés. El punto de equilibrio se mueve de A a B.

Del Modelo de Ingreso-Gasto al Modelo IS-LM. En el modelo de ingreso-gasto, el nivel de inversiones se considera constante (una variable exógena) y determinado por las expectativas a largo plazo de las empresas. Incorporar la función de inversión al modelo de ingreso-gasto vincula la tasa de interés con las variaciones en la demanda agregada (DA) y el ingreso (Y) a través de cambios inducidos en el gasto en inversiones (I).

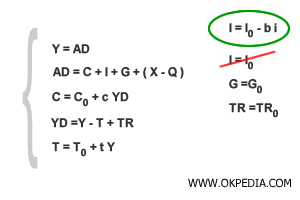
Dado que la tasa de interés (i) también es un factor determinante en el mercado monetario, esto permite identificar un nivel de tasa de interés (i*) que equilibra simultáneamente tanto el mercado real de inversión/ahorro (programa IS) como el mercado monetario (programa LM). La introducción de la función de inversión posibilita la transición del modelo de ingreso-gasto al modelo IS-LM.