Función de Producción

La función de producción establece la relación entre la cantidad de un bien producido (output) y las cantidades de distintos factores productivos empleados en el proceso. Es un concepto clave en microeconomía, utilizado para analizar las decisiones de producción. Matemáticamente, expresa cómo el output (Y) de un bien depende de la combinación de insumos productivos (X) a lo largo de un determinado período.

Y = f ( x₁ , x₂, x₃, ... , x_n)

Dentro de un conjunto de producción Z, la función de producción determina la cantidad máxima de output que se puede obtener con una combinación específica de factores productivos, suponiendo un nivel fijo de capital durante un cierto período. En el caso más simple, con un único producto (Y) y un solo insumo (X), la función de producción se expresa como:

Y_q = f ( x_q )

Cuando se trabaja con un solo insumo y un único output, la función de producción puede representarse gráficamente en un plano cartesiano, donde el output (Y) se sitúa en el eje vertical y la cantidad de insumo (X) en el eje horizontal. A esta representación se le conoce como la curva de producción.

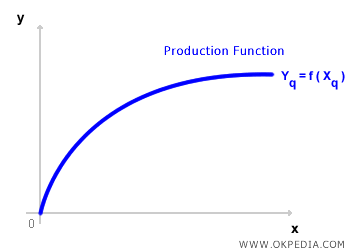
Desde un punto de vista gráfico, la función de producción define la frontera del conjunto de producción. Representa el nivel máximo de output (Y) que se puede alcanzar para cada cantidad de insumo (X). Matemáticamente, la función de producción tiene las siguientes propiedades clave:

• Continuidad. Es una función continua porque tanto el output (Y) como los insumos (X) pueden dividirse en incrementos infinitamente pequeños.
• Monotonicidad. La función es monótona, lo que implica que un aumento en la cantidad de insumo (X) nunca genera una reducción en el output (Y).

La forma de la función de producción depende de los rendimientos a escala. Estos pueden ser:

• Constantes: cuando el output varía en la misma proporción que los insumos.
• Crecientes: cuando el output aumenta a un ritmo mayor que el de los insumos utilizados.
• Decrecientes: cuando el output crece a un ritmo menor que el de los insumos empleados.

En los casos de rendimientos crecientes a escala, la función de producción adopta la siguiente forma:

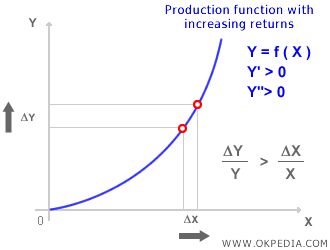
Funciones Homogéneas. Una función homogénea de grado k permite representar distintos tipos de rendimientos a escala. El grado de homogeneidad (k) determina su comportamiento:

• k = 1: Rendimientos constantes a escala.
• k > 1: Rendimientos crecientes a escala.
• k < 1: Rendimientos decrecientes a escala.

Función de Producción en el Corto Plazo. En el corto plazo, la función de producción describe la relación entre insumos y output bajo el supuesto de que el capital y la tecnología se mantienen constantes. Es decir, representa una curva de producción estática. En este horizonte temporal, la empresa solo puede ajustar su producción variando la cantidad de insumos flexibles, como la mano de obra, pero no puede modificar su capacidad productiva ni adoptar nuevas tecnologías. Así, las combinaciones de insumos disponibles están limitadas por la frontera de producción.

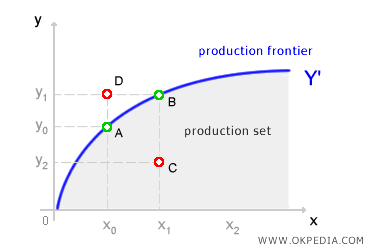
En el gráfico anterior, los puntos A y B se encuentran sobre la frontera de producción y representan combinaciones eficientes de insumos y output, ya que maximizan la producción (Y) para un nivel determinado de insumo (X). En cambio, el punto C está dentro del conjunto de producción y es factible, pero ineficiente, ya que genera un output (Y₂) menor al máximo alcanzable (Y₁) con la misma cantidad de insumo (X₁). Por otro lado, el punto D es inaccesible, pues se encuentra fuera de la frontera de producción.

Progreso Tecnológico. A largo plazo, las empresas pueden ampliar su capacidad de producción e incorporar nuevas tecnologías, lo que incrementa la productividad y la eficiencia. Con el avance tecnológico, la función de producción sufre modificaciones significativas. Gráficamente, si la tecnología permite obtener más output con la misma cantidad de insumos, la función de producción se desplaza hacia arriba, generando una curva dinámica.

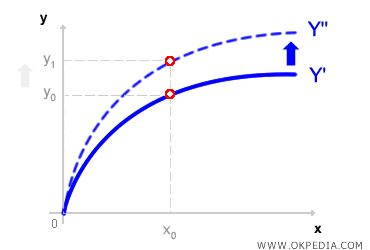
Las innovaciones tecnológicas permiten a las empresas aumentar su producción con los mismos insumos o reducir el uso de recursos sin afectar el nivel de output, mejorando así su eficiencia productiva.