Axioma de transitividad
El axioma de transitividad constituye un principio esencial en la teoría de las preferencias del consumidor, ya que garantiza la coherencia lógica en sus elecciones. Afirma que, dadas tres cestas de consumo - A, B y C - , si el consumidor prefiere A a B y B a C, entonces necesariamente debe preferir A a C. Gráficamente, este axioma implica que las curvas de indiferencia no pueden cruzarse; de lo contrario, se rompería la lógica interna del sistema de preferencias. El siguiente diagrama ilustra un caso hipotético en el que dos curvas de indiferencia se intersectan, comprometiendo la consistencia de las elecciones del consumidor.
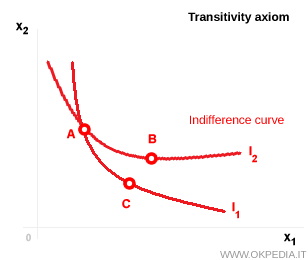
En este ejemplo, las curvas de indiferencia no representan un orden coherente de preferencias. Por ejemplo, las cestas A y B se sitúan sobre la misma curva de indiferencia, $I_2$, lo que indica que el consumidor obtiene el mismo nivel de utilidad de ambas. Lo mismo ocurre con las cestas A y C, que se encuentran en la curva $I_1$. De acuerdo con el axioma de transitividad, esto debería implicar también indiferencia entre B y C. Sin embargo, no es así: la cesta B se encuentra en una curva de indiferencia más elevada que C, lo que la hace claramente preferida. Esta situación conduce a una contradicción evidente:
$$ B \succ C $$ $$ A = C $$ $$ A = B $$
Si el consumidor es indiferente entre A y B, y también entre A y C, no puede racionalmente preferir B a C. Precisamente, el axioma de transitividad es lo que impide este tipo de inconsistencias dentro de un modelo racional del comportamiento del consumidor.
