Caja de Edgeworth
La Caja de Edgeworth es una herramienta gráfica utilizada para analizar la distribución y el intercambio de dos bienes entre dos agentes económicos, así como las condiciones de equilibrio en una economía de intercambio puro. Fue introducida por el economista británico Francis Ysidro Edgeworth y posteriormente perfeccionada por A.L. Bowley. La caja de Edgeworth se puede emplear tanto para estudiar el intercambio de dos bienes (X e Y) entre dos agentes en una economía de intercambio puro (la caja de intercambio de Edgeworth), como para analizar la asignación de factores de producción (K y L) entre dos empresas. En el primer caso, se utilizan curvas de indiferencia entre los dos bienes, mientras que en el segundo se emplean curvas isocuantas para representar la relación entre los factores de producción.
Caja de intercambio de Edgeworth
En el caso de dos agentes económicos (A y B) con dotaciones de bienes (X e Y) y sin actividad productiva, la caja de Edgeworth ayuda a determinar qué cantidad de cada bien intercambiarán los dos agentes, en función de sus dotaciones iniciales y preferencias personales.
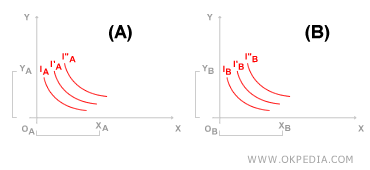
En el primer diagrama cartesiano (Diagrama A), se muestran las curvas de indiferencia del agente A. Este parte de una dotación inicial de XA unidades del bien X y YA unidades del bien Y. En el segundo diagrama (Diagrama B), se representan las curvas de indiferencia del agente B, cuya dotación inicial consiste en XB unidades del bien X y YB unidades del bien Y.
Construcción de la caja de Edgeworth
Para construir la caja de Edgeworth, se rota 180° el diagrama cartesiano del agente B (Diagrama B) y se superpone al Diagrama A. El resultado es un gráfico rectangular con dos orígenes. Desde el origen inferior izquierdo OA, podemos medir las dotaciones e intercambios del agente A, mientras que desde el origen superior derecho OB, hacemos lo propio para el agente B. La caja de Edgeworth se representa visualmente de la siguiente forma:
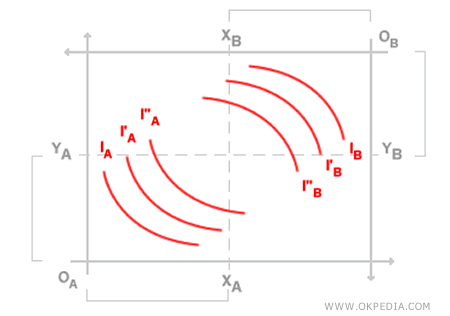
La caja de Edgeworth está formada por dos diagramas cartesianos superpuestos. Ambos diagramas miden las cantidades de los bienes A y B en sus respectivos ejes. Las longitudes de los ejes X e Y en la caja de Edgeworth están determinadas por las dotaciones totales de bienes que poseen ambos agentes. Por ejemplo, la longitud del eje X está dada por la suma de XA + XB, que representa la cantidad total del bien X en manos de los agentes A y B. De manera similar, el eje Y está definido por la suma de YA + YB, que indica la cantidad total del bien Y. Las curvas de indiferencia se mantienen convexas hacia sus respectivos orígenes.
Por ejemplo, las curvas de indiferencia del agente B, IB, son convexas hacia el origen OB, y este siempre prefiere la curva de indiferencia más externa I''B sobre la interna I'B. Esta característica distintiva de la caja de Edgeworth permite observar cómo varían las dotaciones de los agentes a lo largo del proceso de intercambio. La caja de Edgeworth es una herramienta gráfica fundamental en la economía política y en la microeconomía.
Caja de producción de Edgeworth
En la caja de producción de Edgeworth, los ejes cartesianos representan las cantidades de los factores de producción K y L. Las isocuantas en el plano cartesiano muestran las combinaciones de estos factores necesarias para producir los bienes A y B. La suma de KA + KB representa el total de capital (K) disponible en el mercado, mientras que la suma de LA + LB representa el total de mano de obra (L). Según la tecnología de producción utilizada por las empresas (representada por las isocuantas), los puntos en los que las curvas isocuantas se tocan (puntos de tangencia) indican la asignación óptima de capital (K) y trabajo (L).
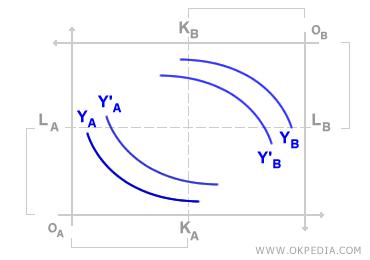
Equilibrio en la caja de Edgeworth. El equilibrio en la caja de Edgeworth se alcanza en los puntos donde las curvas de indiferencia de ambos consumidores son tangentes (el punto de contrato). En estos puntos, la tasa marginal de sustitución entre los bienes es igual para ambos consumidores. Este equilibrio representa una situación óptima de Pareto, es decir, ningún consumidor puede mejorar su utilidad sin perjudicar al otro. El conjunto de todos los puntos de tangencia entre las curvas de indiferencia se denomina curva de contrato. Del mismo modo, el conjunto de puntos de tangencia entre las curvas isocuantas también se conoce como curva de contrato.
